物質の状態　〜体積・密度・モル〜 | 0から始める高校化学まとめ

この単元を学習する前に

まず大事なことは、“固体、液体、気体の性質を学習しておくこと”です。そして、もしわからなくなったら、疑問に思ったら、物質の三態　〜固体、液体、気体〜に戻ってわからないポイントを復習しましょう。

勉強している最中に、自分がやっている問題が固体についての問題なのか、液体なのか、が意識できなくなると理解するのがつらくなります。

まずは、自分がやっている内容が、固体なのか液体なのか、気体についてなのかは常に意識して学習しましょう。

体積、密度は、固体、液体、気体それぞれで算出されますが、高校化学では出題される頻度に偏りがあります。

その偏りに従って学習することはなかなか難しいので、この単元は問題集の問題を多く解くことによって習得していきましょう。

計算の力が必要とされる

この単元は計算を多く使います。とはいえ、難しい計算を使うわけではありません。重要なのは、どの計算パターンを使うのか、という判断です。

どれをどれで割るのか、かけるのか、というパターンを状況によって使い分ける力が必要です。問題を多くこなすことによってこのパターンの使い分けを習得するのが近道といえますが、まずは以下の流れで問題を解いていくとスムーズに問題の解答力がアップします。

・体積、密度の算出の仕方。
・モルを使った計算。
・モルと体積、密度を関係させた問題。

この分類をまず意識して、この単元の学習に取りかかりましょう。

便利な公式、考え方を身につけ、勘違いポイントを消そう

計算問題を解くための便利なツールというものがあります。これは、覚えておくと考える時間が節約でき、解答にたどりつくまでの時間を節約できます。

試験の時に、時間がかかると焦りを生みます。この焦りは計算問題の大敵です。まずは1つ、絶対に覚えておいて欲しい計算のツールを紹介します。

割合を計算するときの便利ツール

高校生、大学生の傾向として、割合を使った計算が苦手というものがあります。

9 : 3 = X : 6 のXを求める時に、戸惑う人は多く、最近の大学では、入学してすぐにこういった高校の基礎的な事柄を教える講義を設定することが多くなっています。

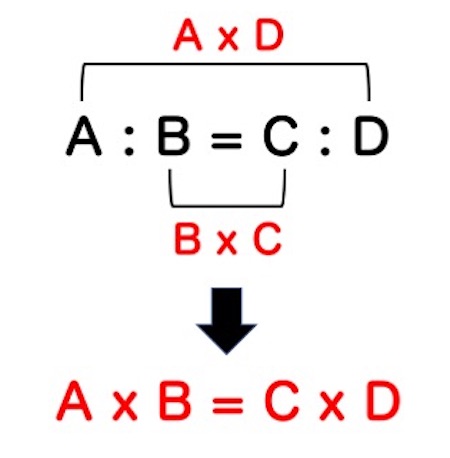
上に示した図は、内項の積 = 外項の積を表しています。イコールを挟んで、外側同士を掛け算したものと、内側同士を掛け算したものは等しくなります。

つまり、9 : 3 = X : 6は、9 x 6 = 3Xになり、3X = 54、よってX = 18。これによって、
9 : 3 = 18 : 6が完成します。

この内項の積 = 外項の積は覚えておくと非常に便利です。

勘違いに注意

体積、密度で勘違いしやすいポイントに、cm³からm³への変換があります。

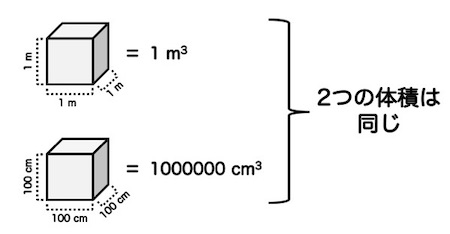
1 mは100 cmですが、1 m³は100 cm³ではありません。

1 m³は、1 m × 1 m × 1 mの立方体の体積です。これをcmに変換すると、100 cm × 100 cm × 100cmですので、1000000 cm³となります。

ここは以外と勘違いするポイントですので、しっかりと頭に入れておきましょう。

単位は計算のヒントが隠れている

計算問題をこなしていくことによって、計算パターンは自然と身につきます。しかし、その計算パターンの引き出しは持っていおいた方が安心です。

この引き出しは、“算出しようとする値の単位”を把握すると開けやすくなります。なぜなら、単位には計算のヒントが隠されているからです。

問題によっては、単位を書いてあるものがあります。例えば、mg/mlを求めよ、という問題です。

こういった問題であれば、mg/ml = mg ÷ ml と考えればよいわけです。なんてことはないのですが、頭に入れておくと、この単元以外にもいろいろと便利です。

多くの人が苦手とする“モル”

モルは、多くの人が苦手とする単位です。

重さや体積は、目で見たり、持ったりして実感できるのですが、モルという単位は人間の五感ではなかなか実感できません。

まずはモルの定義を整理しましょう。モルは、molで表されます。

・物質量を表す単位。
・鉄なら、鉄の原子6.02 × 10²³個が1 molである（6.02 × 10²³はアボガドロ定数と言われる）。
・組成が明らかになっている粒子、6.02 × 10²³個で構成された系が1 molである。

そして、1 molの物質の重さは、原子量、分子量によって決められています。

原子量、分子量とは、炭素原子1個を12の質量があるとしたときに、比によって計算される物質固有の量です。

質量と質量の“比”ですので、単位がありません。こういう数値は、無次元量と言われます。

具体的に、二酸化炭素、CO₂で考えてみましょう。

二酸化炭素の分子量は、原子量が12の炭素が1個、原子量が16の酸素が2個、つまり44になります。

となりますと、二酸化炭素の分子、6.02 × 10²³個は1 mol。そしてその質量は44 gとなります。

つまり、「ある分子 1mol」＝ 「6.02 × 10²³個のその分子」 = 「分子量から算出された質量（分子量にgを付ければその質量と等しくなる）」となります。

6.02 × 10²³ はアボガドロ定数です。原子量、分子量と同様に無次元量ですので単位がありません。

ただし、6.02 × 10²³ / mol（または6.02 × 10²³ mol^-1）と表されることもあります。

これは、1 molに6.02 × 10²³個の粒子が含まれているので、「6.02 × 10²³個 / 1mol」という意味であることを押さえて下さい。

モル（mol）を使った濃度計算

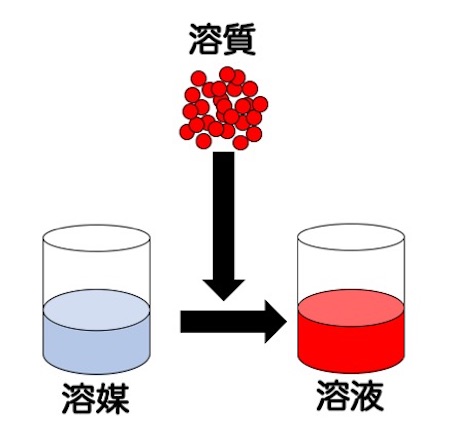
モルを使った濃度計算を理解するには、溶液、溶質、溶媒の区別をしっかりすることが重要です。もし、曖昧ならば単元を戻って復習しましょう。

まず、溶媒は「溶質を溶かす液体」です。そして、溶質は「溶媒に溶かす物質」。溶質が溶媒に溶けると、「溶液」の完成です。この区別をしっかりした上で、モルを使った濃度を学習しましょう。ポイントは、割り算をするとき、割るものが溶液なのか溶媒なのか、です。

質量パーセント濃度

（溶質の質量）÷（溶液の質量）× 100（%）によって計算されます。パーセント濃度ですので、単位はパーセント（%）になります。

質量を質量で割るので、100を掛ける前の値の単位は、g / g、g / kgなど、分母も分子も重さを表す単位で構成されます。

モル濃度

溶液1 Lに、溶質がどれだけ溶けているかをmolを使って算出します。溶質の量がmolで表されます。

（溶質の物質量：単位はmol）÷（溶液の体積）＝　モル濃度（mol / L）となります。この1Lあたりのmol量は、1 mol/L = 1 M（モラーと読みます）と表されることもあります。例えば2 Mですと、1 Lに2 molのその物質が溶けているということになります。

質量モル濃度

質量モル濃度は、凝固点降下、沸点上昇の算出の際に使う値です。誤解しやすい算出方法ですので、きちんと覚えましょう。

（溶質の物質量：単位はmol）÷（溶媒の質量）＝　質量モル濃度（mol / kg）です。ここで注意点は、割る値が、“溶媒の質量”であることです。溶液の質量ではありません。

以上に挙げた濃度が何の値で割られているのか、は確実に覚えておく必要があります。質量パーセント濃度は溶液（溶媒 + 溶質）の質量、モル濃度は溶液の体積、そして質量モル濃度は、“溶媒”の質量で割られている、をしっかり覚えましょう。

固体を液体に溶かす、という考え方だと比較的わかりやすいのですが、液体を液体に溶かす、という問題も時々見かけることがあります。

100 %のエタノール ○ mlを△ mlに溶かした場合の濃度などがその問題に該当します。80 %のエタノール、70 %のエタノールなど、元々の濃度を変えて作問されることがありますので、こういう問題を見かけたら飛ばさずにやってみましょう。

原子量、分子量は覚えるよりも使い方と代表的な化合物の組成をしっかり学習

また、モルを扱う問題では、原子量、分子量が計算に必要になります。二酸化炭素などの分子量を覚えておいてもいいとは思いますが、ほとんどの問題で、原子量の指定があります。

これは同位体の存在があるためで、炭素の原子量はとりあえず12となっていますが、実際は12.0107です。他の原子でも同様に、酸素は一般的に原子量16とされていますが、正確には15.9994です。

これによる混乱を防ぐために、問題では「原子量は、C = 12、O = 16として計算せよ」などの情報が書かれる場合がほとんどです。

また、この記事ではアボガドロ定数を　6.02 × 1023 としていますが、問題によっては、「6.0 × 1023とする」という注意が書いてあることもあります。問題文は注意深く、全て読み切ってから解答に取りかかって下さい。

そうなりますと何が重要になってくるのでしょうか？

重要なのは、二酸化炭素の分子量を覚えるよりも、「二酸化炭素は1つの炭素と2つの酸素でできている。つまりCO2である。」という情報を頭に入れることです。

モルを扱った問題を解くために、代表的な化合物の組成は知っておくことが重要です。問題を解きながら、覚えていない化合物が出てきたときには、その時にしっかり頭に入れるようにしましょう。

また原子量、分子量は、数値を覚えるよりも、それらを使ってどういう計算をすればどういう値が出るのかをしっかりと学習しましょう。

代表的な化合物の組成が書けること、原子量、分子量をどう使えばどういう値が出るのかを押さえることが優先事項です。

モルと気体

モル体積は、気体における代表的なモル計算です。

単位は、m3 / molで表されます。計算は、モル質量（kg / mol）÷ 密度（kg / m3）の式を使います。ここで、単位を使ってこの計算を整理してみます。

（kg / mol） ÷ （kg / m3） = （kg / mol） × （m3 / kg）= (m3 / mol)

1 molあたりの体積が算出されます。つまり、その気体が1 molあると体積はどのくらいか？を表します。また、1 mol = 6.02 × 1023個の分子ですので、その分子が6.02 × 1023個あると、どのくらいの体積か？も表しています。また、m3 / molのm3は、L（リットル）で表されることもあります。

この体積は、物質によって大差なく、理想気体の状態でおおよそ22.4 Lの体積です。高校化学のうちは、この単元の問題の多くは理想気体で出題されます。ですので、理想気体の状態方程式、pV = nRT（p = 圧力、V = 体積、n = 物質量、R = モル気体定数、T = 熱力学定数）はここで覚えましょう。

ここで、ボイルの法則、シャルルの法則、ゲイ＝リュサックの法則、そしてそれらを統合した、ボイル＝シャルルの法則も学習しておくと、比較的難易度の高い問題にも対応できます。

モルは意外と便利

モルはややこしい計算問題が多いという印象がありますが、実は便利なツールです。ここで、熱力学的な単元において、覚えておきたいモルを使った情報があります。

固体、液体、気体の物質の三態を学んだとき、固体から液体への融解、液体から気体への蒸発という言葉を覚えたと思います。

これに関連した、融解熱、蒸発熱は、モルを使った言葉で定義されています。

融解熱：1 molの固体が液体になるときに必要な熱量
蒸発熱：1 molの液体が気体になるときに必要な熱量
凝固熱：1 molの液体が固体になるときに放出する熱量
凝縮熱：1 molの気体が液体になるときに放出する熱量
昇華熱：1 molの物質が昇華するときに必要な熱量

これらは、物質の変化における熱の出入り、エネルギーの出入りを表した言葉です。この1 molという所がポイントで、エネルギーの出入りの計算問題が出たときに、この情報を知っていれば、すんなり解ける問題があります。

さらに難易度の高い問題を解けるようになりたい場合は、上の情報を押さえた後に、ヘスの法則を学習して下さい。

物理の単元によっては、モルを知っていると理解がしやすいものがあります。熱力学の単元はその代表例です。モルが絡む熱力学の法則を、ここで習得しておくと、化学だけでなく物理にも効果があります。

熱力学第ゼロ法則：物体AとBが熱平衡で（物体間の熱移動が止まった状態）、物体BとCも熱平衡にある場合、AとCも必ず熱平衡である。

熱力学第一法則：物体に外部から加わった仕事と熱量の和は、内部エネルギーの増加に等しい。

熱力学第二法則：熱は高温から低温に移動し、その逆は起こらない。

熱力学第三法則：絶対零度ではどんな物質のエントロピーも零になる。

このうち、モルと特に関連が深いのは、熱力学第一法則です。1 molあたりの熱量を与えられて、質量で表されている物質の総熱量を算出する問題などが出題される頻度が高くなっています。

　おすすめの勉強アプリはコチラ